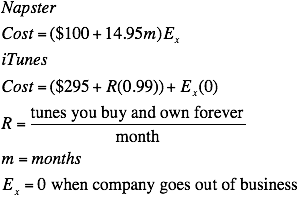- 2005.02.15
I did
the math Napster suggests, but like all poorly trained high school
students, they have set down the arithmetic without showing the
formulas that explain how you know what to multiply and divide.
Upon further consideration, we here at the Lite Side have done a
sophisticated mathematical model based on algebra rather than on
arithmetic, which has generated a nice set of equations we like to
call
Napster's Math Doesn't Account for the
Extinction Factor
Consider the following. A Napster user, having finally found a
$100 Napster-to-go player that actually, you know,
functions, spends $14.95 per month to download and listen to
as many songs as they like. This could potentially be several
thousand songs if they never listen to anything twice and listen to
music eight hours a day (as we all know that young people are wont
to do).
iTunes, on the other hand, has a higher up front cost because
iPods are more expensive (let's say $295, for example) and users
must pay $0.99 for songs they keep forever. A person could purchase
a certain number of songs per month (call this the song
rate, R) and after a while, they could accumulate enough
songs to listen to a song no more frequently than once per
month.
It would take a while, though, depending on your assumptions it
might take as long as five to ten years of steady purchases to have
enough songs on your iPod that you wouldn't need to listen to
anything twice in a month.
The factor that is missing is the extinction factor,
Ex. The extinction factor is a flag that equals 1
when a company is solvent and 0 when it is not.
Apple's demise has been predicted
frequently for a long time now, but let's suppose it
applies to Napster as well.
When Ex for Napster goes to zero (let's say in about
three years), the total tunes you will have available for listening
is . . . well, zero.
When Apple's Ex goes to zero (we all hope it won't,
but you never can tell about the future) the total number of songs
you will have is . . . not zero.
Mathematically, that looks like the following:
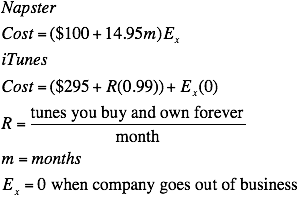
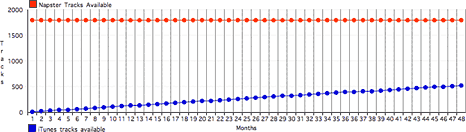
Consider this graph, where neither company goes out of business
in the next four years:
But suppose both companies go bankrupt and out of business in
three years. Look what happens:
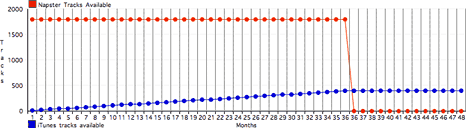
Which is a fancy way of saying what everyone else has been
saying: When Napster goes belly-up (not if - when) your
investment is toast. Whereas even if Apple gets sold to Disney or
something, you will still have your iTunes as long as your
equipment holds out.
And we're not even getting into probability here - the odds of
Apple going bankrupt in three years are pretty slim, whereas
Napster, as a company name, has already tanked once. (Not with the
same people, but, hey, when you buy damaged goods, you get the good
with the bad.)
I hope this mathematical model helps you understand that your
iTunes expenditure is a really good return on investment because
you actually have a lot more freedom to do your own thing. You
could even use iTunes for a while, then switch to another system,
and you'd still own your iTunes, DRM restrictions
notwithstanding (that's true for Napster, too, y'know), whereas
once you're in Napster you're trapped forever unless you want to
start over with another vendor.
Tonight's homework: Assume the rate of music buying is inversely
proportional to the number of songs already owned (you've bought
everything you like in the genre already) and directly proportional
to the rate of new high-quality music production by the music
industry (which must be a small, positive number . . .
right? Right?) and rebuild this simulation making reasonable
assumptions about what a typical person already owns.